公司名稱：南昌孟龍實業(yè)有限公司
聯(lián)系人：劉經(jīng)理(13767010068)
固定電話：0791-86653069
文本傳真：0791-86653269
電子郵箱:menglonggj@126.com
公司地址:江西省南昌市灌嬰路金潤二期6棟32-33號
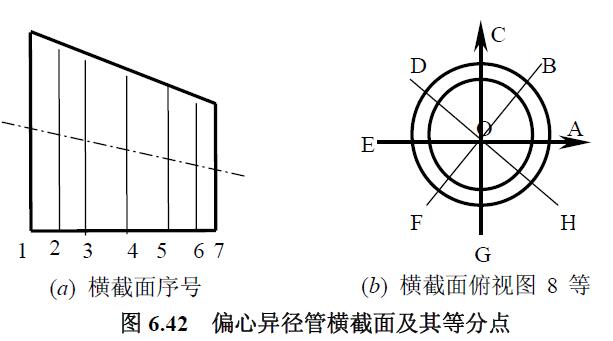
應(yīng)變測量點見圖 6.42 所示的異徑彎管7 個徑向橫截面與其平底側(cè)G、偏心側(cè)C、中性線A 這三條特征經(jīng)線的交點。由于各應(yīng)力曲線圖中的應(yīng)力值由所測應(yīng)變按彈性應(yīng)力公式計算，而實際應(yīng)變已可能包括塑性應(yīng)變，因此，曲線中的應(yīng)力均稱為名義應(yīng)力。同時，各應(yīng)力曲線圖中標(biāo)識的大端和小端，對偏心異徑管而言是指軸向高度等于零處和異徑管高度處，由于這兩個測量位置的應(yīng)變片貼在焊縫上，焊縫的力學(xué)性能不清楚，因此，所測量得的名義應(yīng)力值僅供參考。
6.4.1 偏心異徑管試件的基本情況
偏心異徑管①硬度及壁厚實測值見表6.9 和表6.10。橫截面的序號和等分點的字母方位如圖6.44 所示，偏心異徑管的幾何外型與標(biāo)準(zhǔn)有明顯偏差。
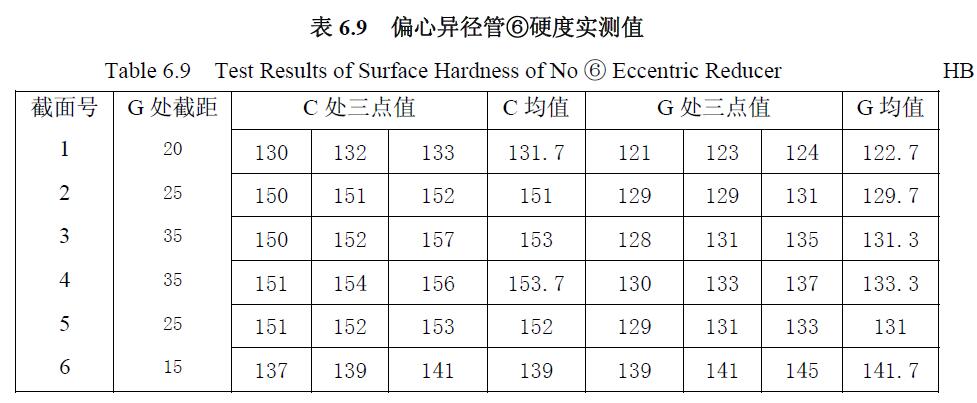
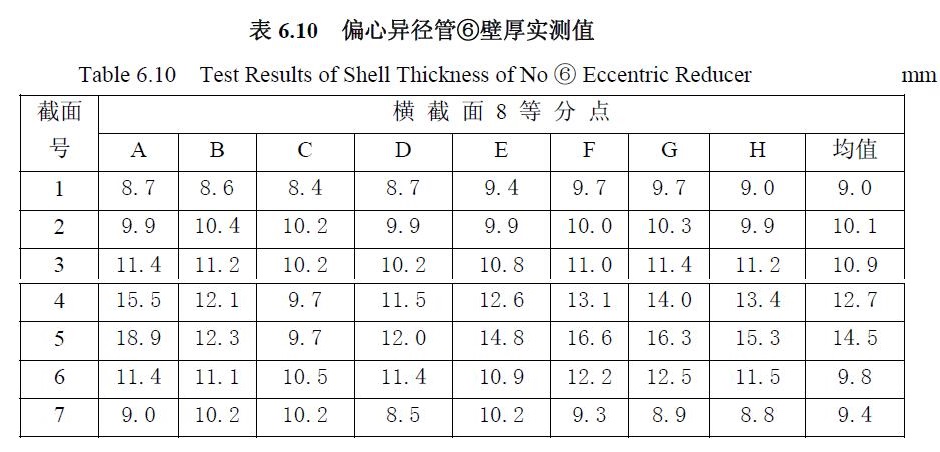
偏心異徑管②試驗后其過軸線剖面見附錄圖A12，其偏心側(cè)和平底側(cè)的壁厚均是中間較厚而大小兩端較薄，平底側(cè)大端因為外凸而顯得不平底。
6.4.2 內(nèi)壓作用
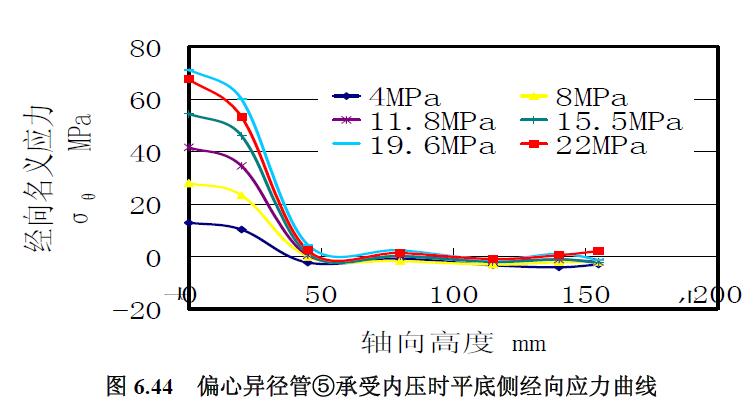
1) 應(yīng)力曲線 分析偏心異徑管⑤承受內(nèi)壓的實驗曲線圖6.43 和圖6.46：(1) 平底側(cè)和中性線的應(yīng)力曲線的形狀走勢基本相同，并且大端的應(yīng)力曲線分明顯分散，中間高度和小端的應(yīng)力曲線十分集中。(2) 經(jīng)線上的環(huán)向應(yīng)力曲線與經(jīng)向應(yīng)力曲線兩者的形狀走勢基本相同。(3) 偏心側(cè)和中性線靠近大端的經(jīng)向應(yīng)力為低水平的壓應(yīng)力，其余應(yīng)力均是拉應(yīng)力。(4) 偏心側(cè)的環(huán)向應(yīng)力表現(xiàn)出大端處的環(huán)向應(yīng)力較小端處的環(huán)向應(yīng)力小，與壁厚分布有關(guān)。
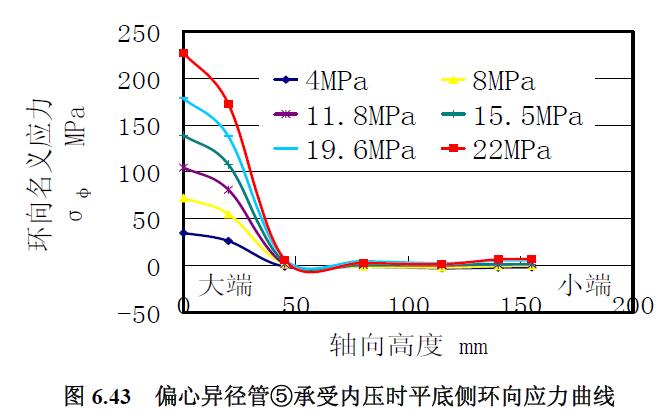
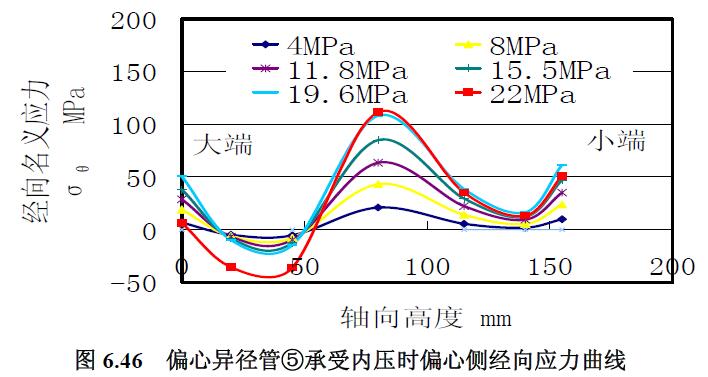
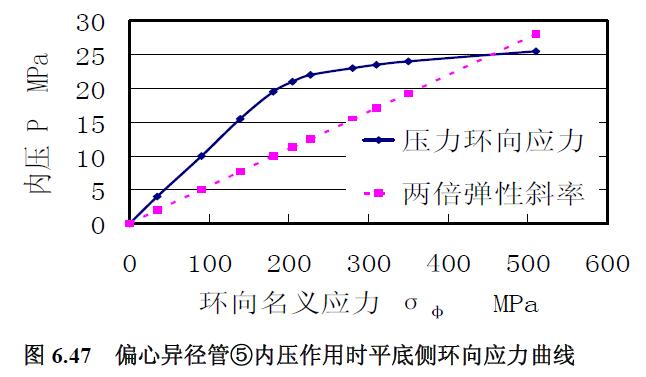
2) 極限載荷分析 平底側(cè)內(nèi)壓環(huán)向應(yīng)力曲線與中性線的內(nèi)壓環(huán)向應(yīng)力曲線基本重合一致，根據(jù)到22MPa 的內(nèi)壓環(huán)向應(yīng)力曲線趨勢的延長曲線圖6.47 求得極限內(nèi)壓為25MPa。
6.4.3 彎矩加載試驗
偏心異徑管②和⑥分別進行了專門的彎矩試驗，但兩者的彎矩方向相反。
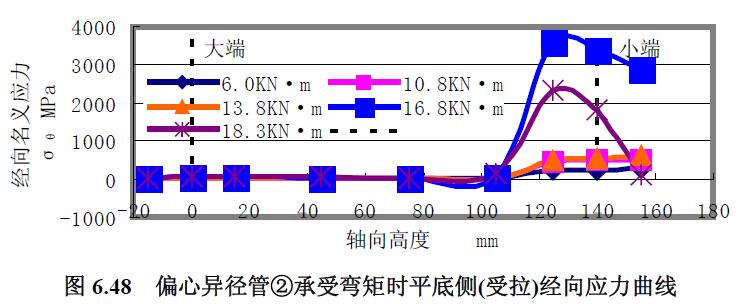
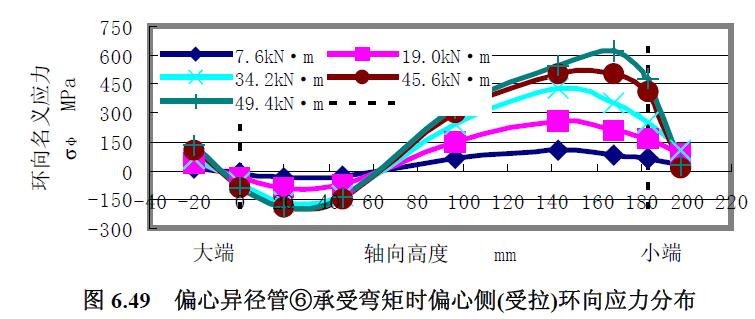
1) 偏心異徑管⑥的實驗曲線 此時偏心異徑管②的偏心側(cè)受壓，對應(yīng)力曲線圖6.48和圖6.49 分析：(1) 偏心異徑管在彎矩單獨加載作用下平底側(cè)、偏心側(cè)、中性線的應(yīng)力分布與其在相同方向彎矩和內(nèi)壓組合作用下的應(yīng)力分布比較，兩者的趨勢基本一致。(2) 在承受彎矩拉伸作用的平底側(cè)其經(jīng)向應(yīng)力分布曲線與中性線的經(jīng)向應(yīng)力分布曲線趨勢一樣，只不過在小端外的其他區(qū)域，平底側(cè)的經(jīng)向應(yīng)力為拉應(yīng)力，中性線的經(jīng)向應(yīng)力為壓應(yīng)力，但是兩者的拉應(yīng)力和壓應(yīng)力數(shù)值大小基本相等且接近零。(3) 經(jīng)向應(yīng)力要比環(huán)向應(yīng)力大。
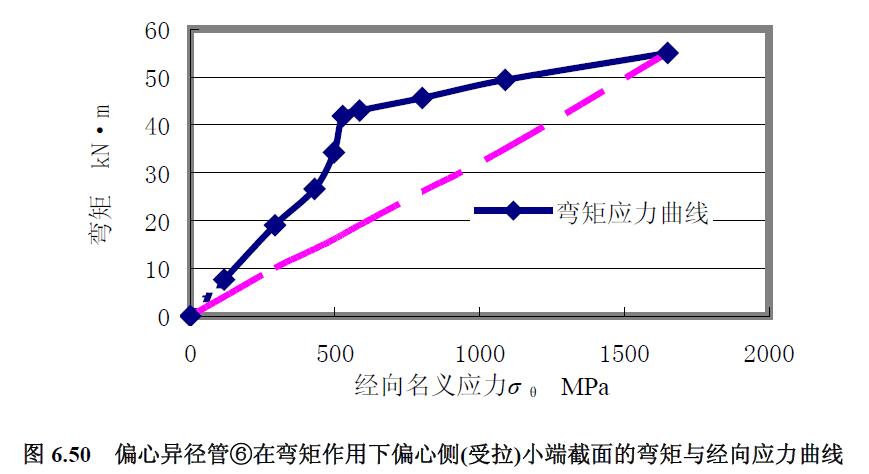
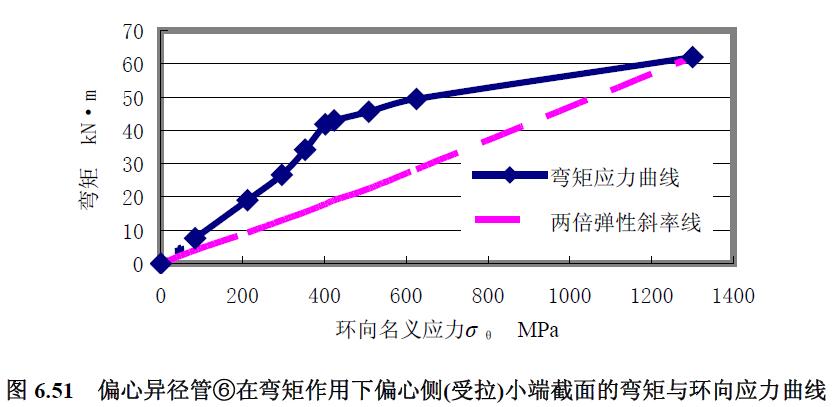
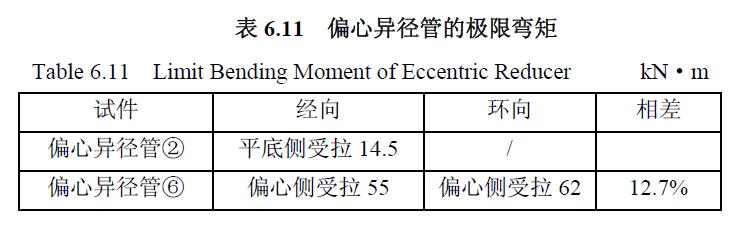
2) 彎矩應(yīng)力曲線 由圖6.50 和圖6.51 求偏心異徑管⑥的極限彎矩如表6.11 所示。
6.4.4 扭矩試驗
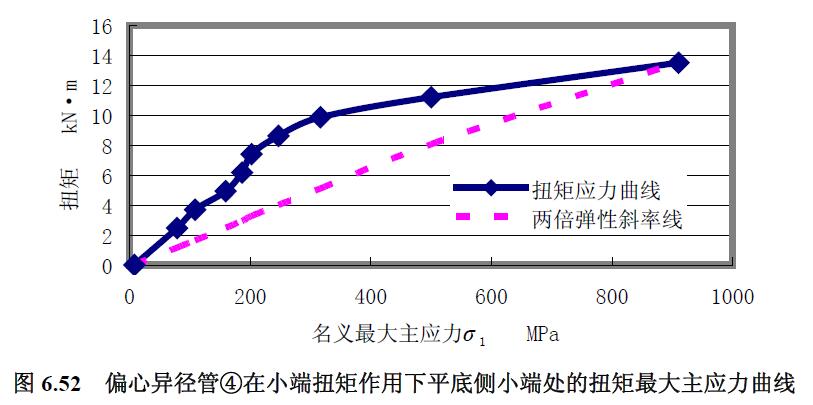
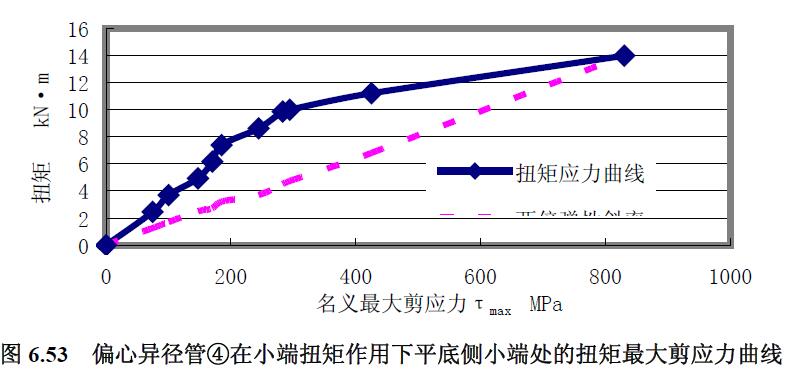
分析偏心異徑管④扭矩作用的應(yīng)力曲線：(1) 從大端直至管件中間高度，應(yīng)力均由較低水平開始，非常緩慢地增大，接近管件小端時應(yīng)力水平陡然增大至高水平。(2) 中性線和平底側(cè)的最小主應(yīng)力為壓應(yīng)力，其余應(yīng)力為拉應(yīng)力。(3) 除接近小端處外，中間段和大端各曲線集中在一起。再分析由平底側(cè)小端應(yīng)力變化繪制扭矩應(yīng)力曲線圖6.52 和圖6.53，由最大主應(yīng)力、最小主應(yīng)力和最大剪應(yīng)力求得的極限扭矩均為13.5kN·m。
