www.gallerie.cn-大地资源高清在线视频播放,中文无码一区二区不卡αv,办公室被CAO的合不拢腿,精品精品男人的天堂久久国产

?

    由于各應力曲線圖中的應力值由所測應變按彈性應力公式計算，而實際應變已可能包括塑性應變，因此，曲線中的應力均稱為名義應力。同時，各應力曲線圖中標識的大端和小端，對異徑彎管而言是指經(jīng)向轉角等于零處和等于90°處，由于這兩個測量位置的應變片貼在焊縫上，焊縫的力學性能不清楚，因此，所測量得的名義應力值僅供參考。

6.3.1 異徑彎管試件的基本情況

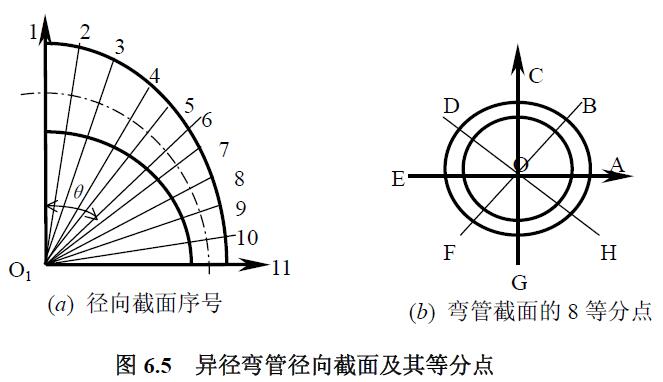
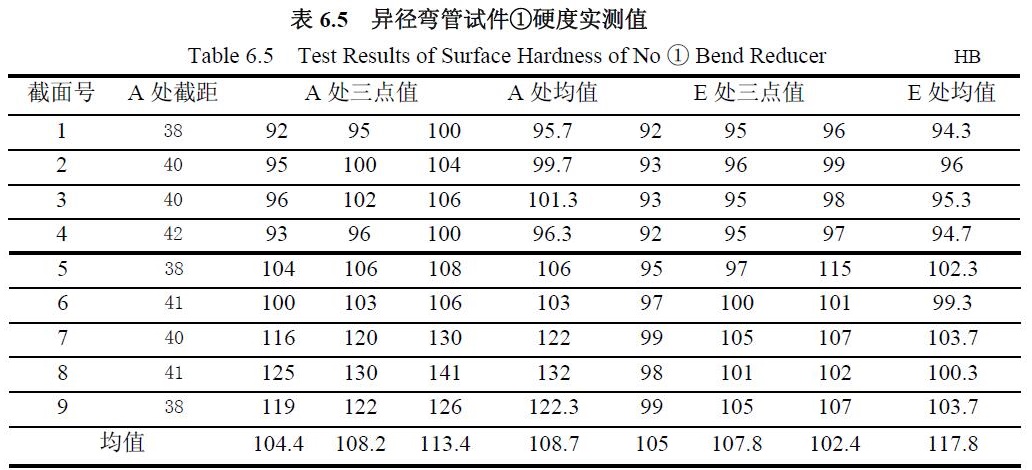
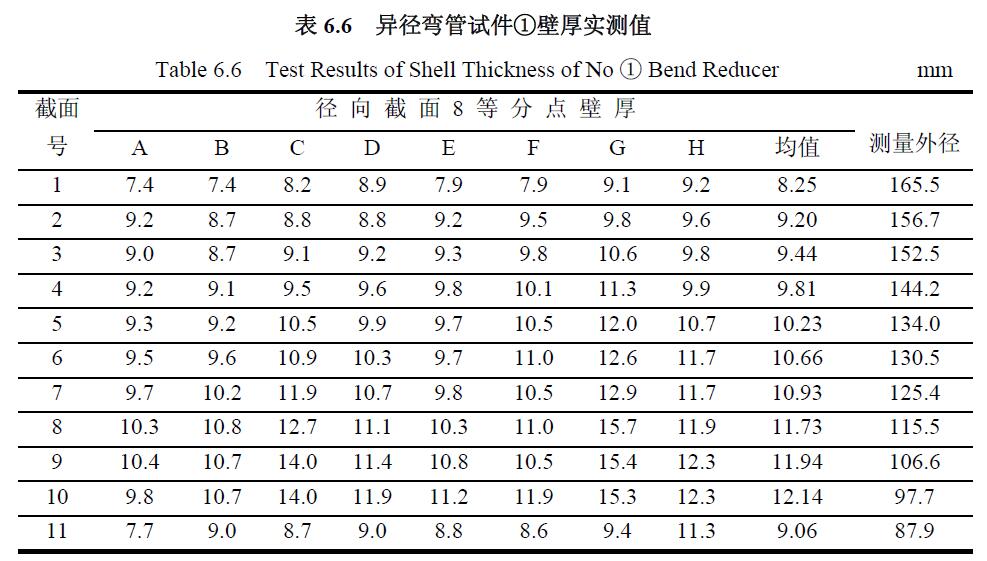
    異徑彎管試件硬度及壁厚實測值只列出件號①的測量結果，分別見表6.5 和表6.6。分別把超聲探頭分隔面與彎頭軸線平行和垂直時測得的兩種數(shù)值，計算兩者平均值相差不到0.5%，后者略高。表6.5 中的壁厚值是探頭分隔面與彎頭軸線垂直時測得的壁厚值(以下同)，表中的徑向截面的數(shù)字序號和等分點的字母方位如圖6.5 所示。

6.3.2 內(nèi)壓試驗

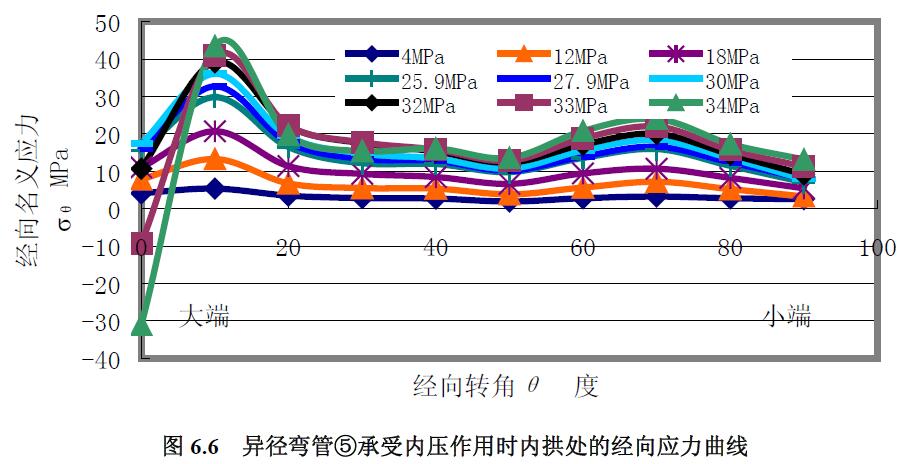
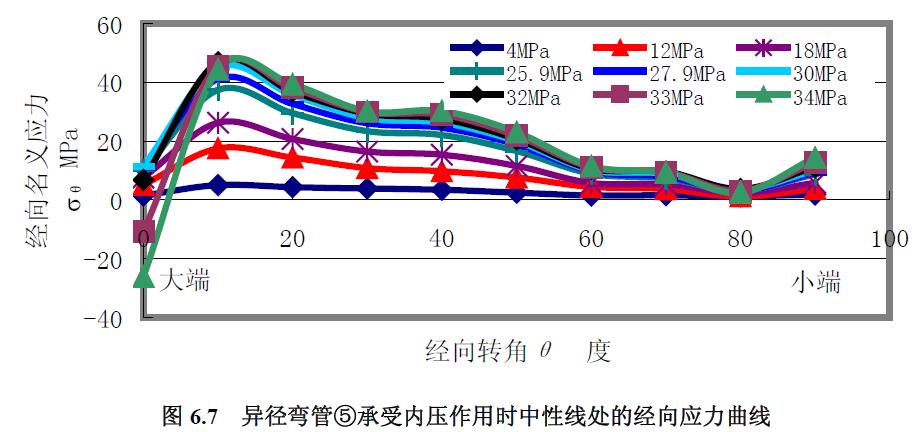
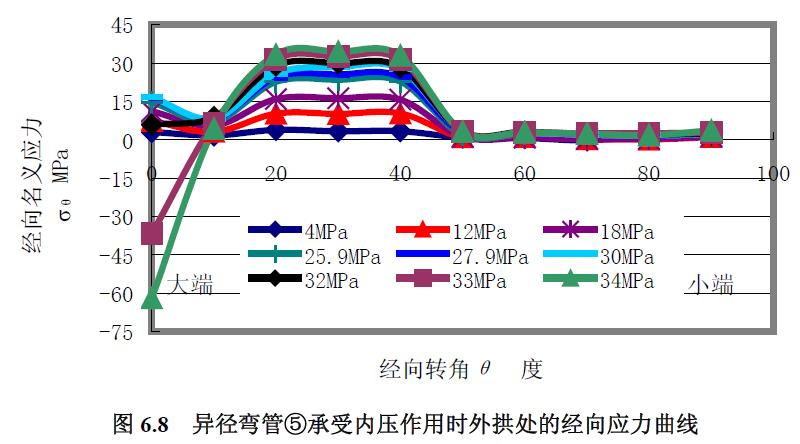
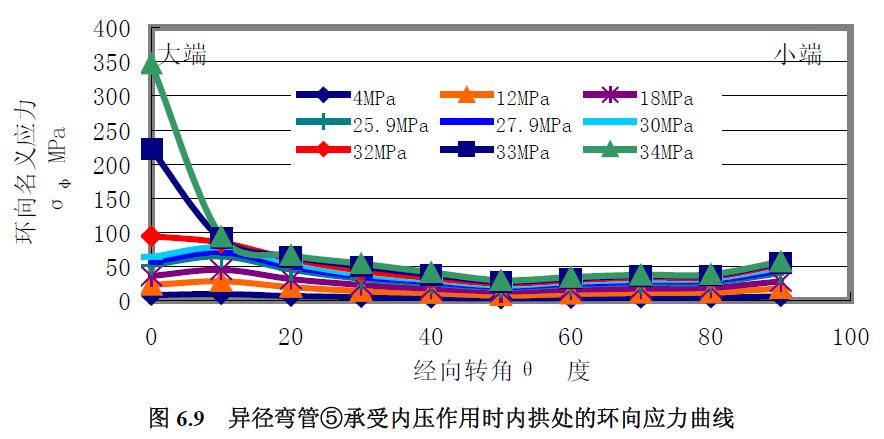
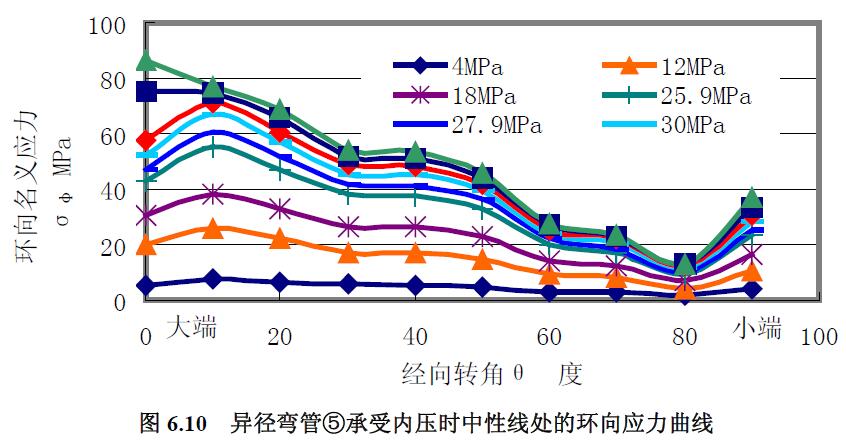
    異徑彎管①、②、③、④和⑥均在進行其他載荷的實驗前了進行了低壓下的應力測試，而異徑彎管⑤則進行了專門的內(nèi)壓應力測試，應變測量點見圖6.5 所示的異徑彎管10 個徑向截面與其內(nèi)拱G、外拱C、中性線A 這三條特征經(jīng)線的交點，結果見圖6.6 至圖6.11。

    1) 經(jīng)向應力 分析結果：(1) 內(nèi)壓增大，經(jīng)向應力曲線變得陡峭。(2) 經(jīng)向應力均為拉應力，從最大內(nèi)壓時的應力水平看，最大經(jīng)向應力從大到小的順序依次為內(nèi)拱、中性線、外拱。(3) 不同內(nèi)壓時的應力曲線集中程度從高到低的順序看，依次為內(nèi)拱、外拱、中性線。

    當內(nèi)壓較高時，大端環(huán)焊縫因為與直管及異徑彎管的材料性能差異而表現(xiàn)出較高的抗變形能力，焊縫兩側的徑向位移較大而相對地使焊縫在經(jīng)向受到壓縮，經(jīng)向應力由內(nèi)壓較低時的拉應力轉變?yōu)閴簯ΑＡ硗猓捎诋悘綇澒苤圃旃に嚨木売桑挥谕夤安⒖拷《艘欢尾牧系腍B 硬度值要比外拱線上靠近大端一段材料或中性線的HB 硬度值要高出約15%，其抗變形能力也較強，因此，外拱靠近小端段的經(jīng)向應力和環(huán)向應力曲線隨內(nèi)壓的增加變化不大。

    2) 環(huán)向應力針對異徑彎管⑤有：(1) 環(huán)向應力曲線與經(jīng)向應力曲線具有相同的走勢。(2) 環(huán)向應力水平尚未達到經(jīng)向應力水平的兩倍。(3) 不同經(jīng)線處的環(huán)向應力相比，內(nèi)拱處環(huán)向應力最大，中性線環(huán)向應力次之，外拱處環(huán)向應力最小。

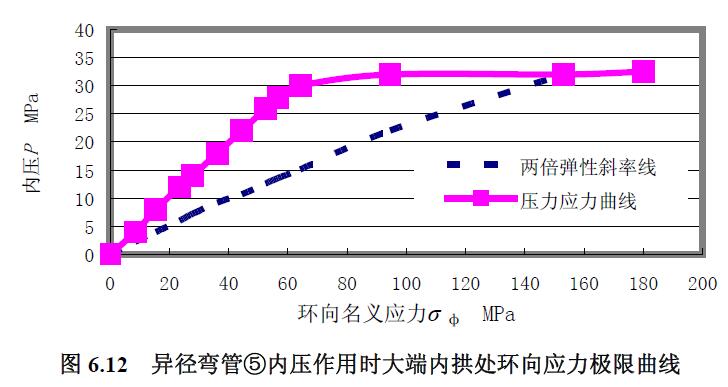
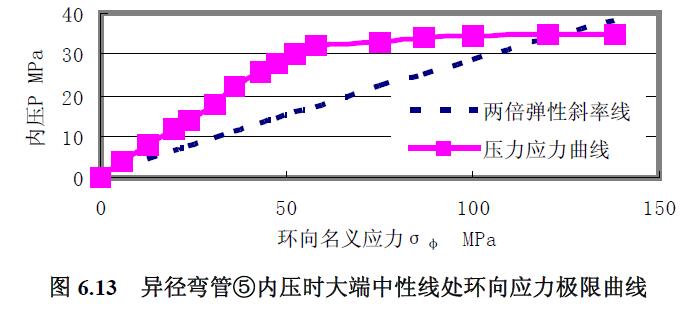
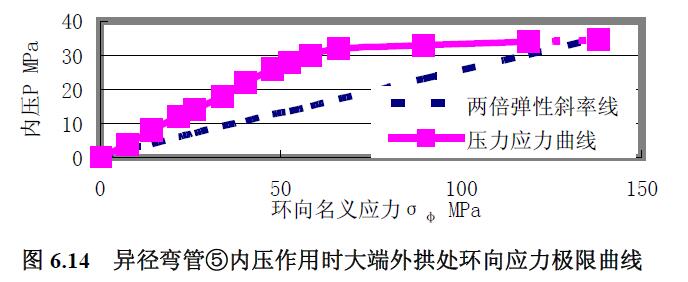
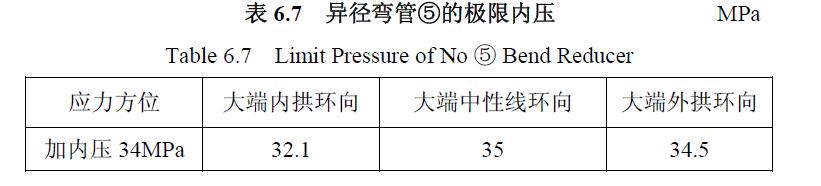
    3) 極限載荷曲線比較分析 由異徑彎管⑤承受內(nèi)壓時大端內(nèi)外拱及中性線上的環(huán)向應力繪制內(nèi)壓應力極限曲線見圖6.12 至圖6.15，求得極限內(nèi)壓見表6.7，表中中性線處較外拱處的極限內(nèi)壓低約1.4 %，是因為壁厚差異、內(nèi)外拱方向為長軸的橢圓度影響。

6.3.3 開彎矩試驗

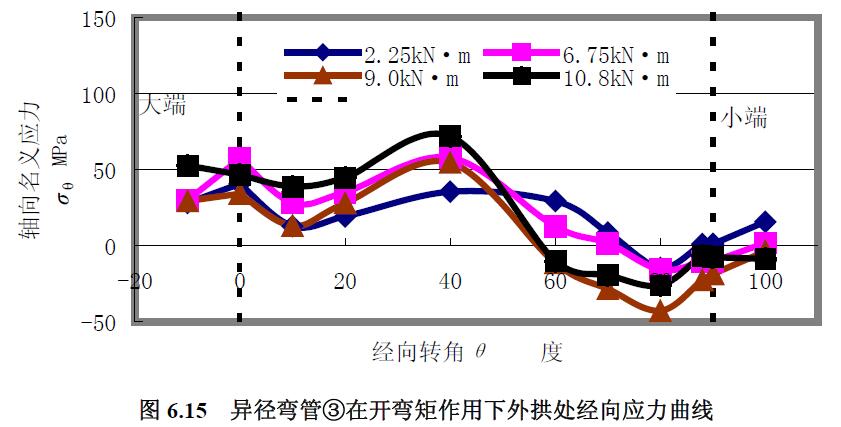
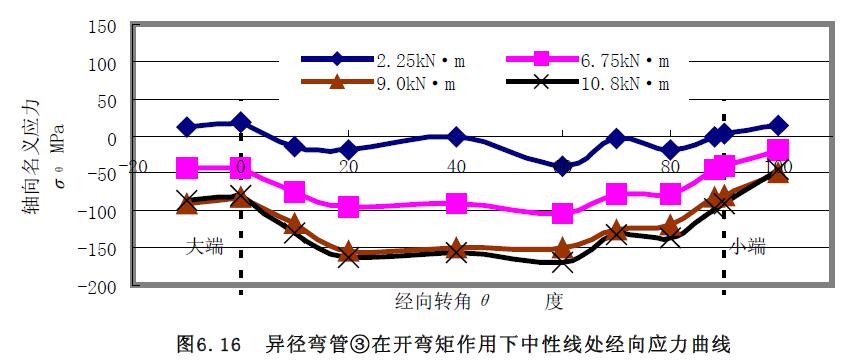
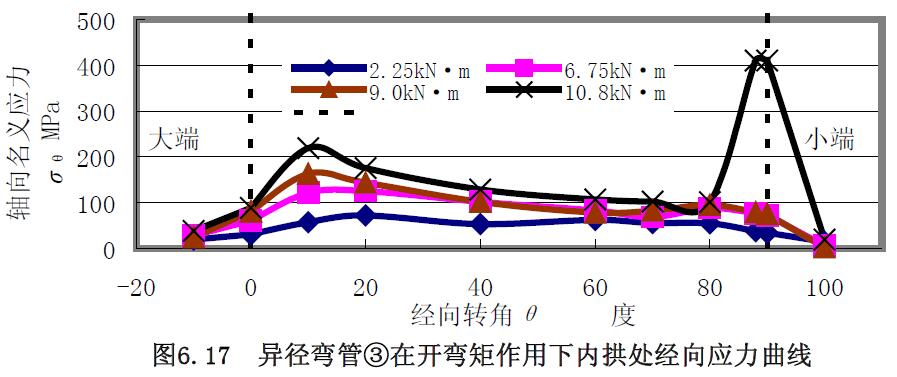
    1) 應力曲線 異徑彎管②和③組合試件進行了小端開彎實驗，對異徑彎管③的實驗結果曲線圖6.15～圖6.20 分析：(1) 經(jīng)向應力在外拱處的大端較小端的大，在內(nèi)拱處均是拉應力，在中性線處，大小兩端的經(jīng)向應力始終基本相等，但是，隨著壓力的增大，中間段的經(jīng)向應力要比大小兩端的數(shù)值要大，且均是壓應力。（2）內(nèi)拱處的環(huán)向應力均是拉應力，外拱處的環(huán)向應力隨著彎矩的增大均是壓應力，在中性線處是壓應力。

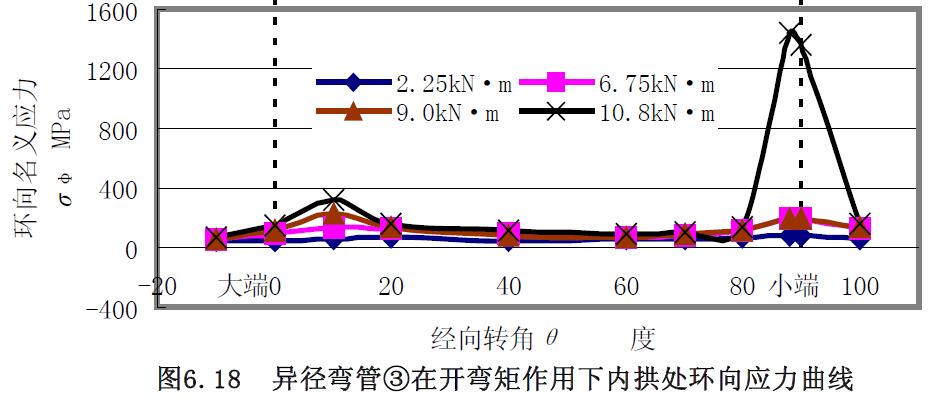
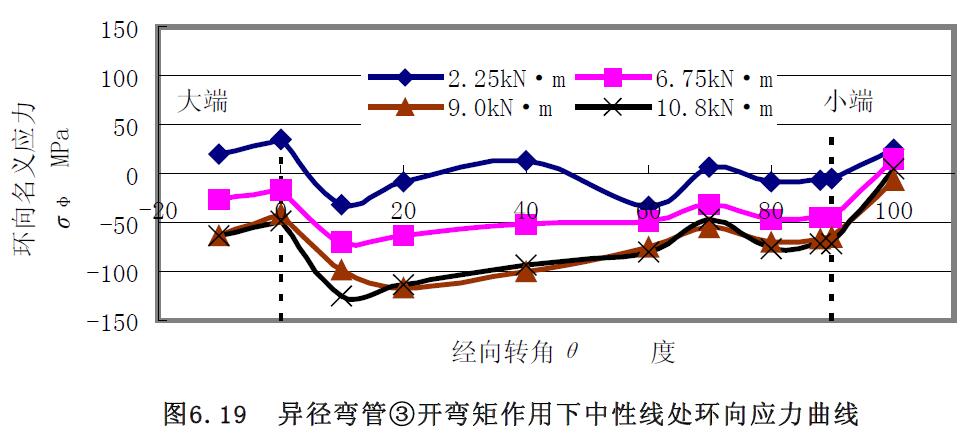
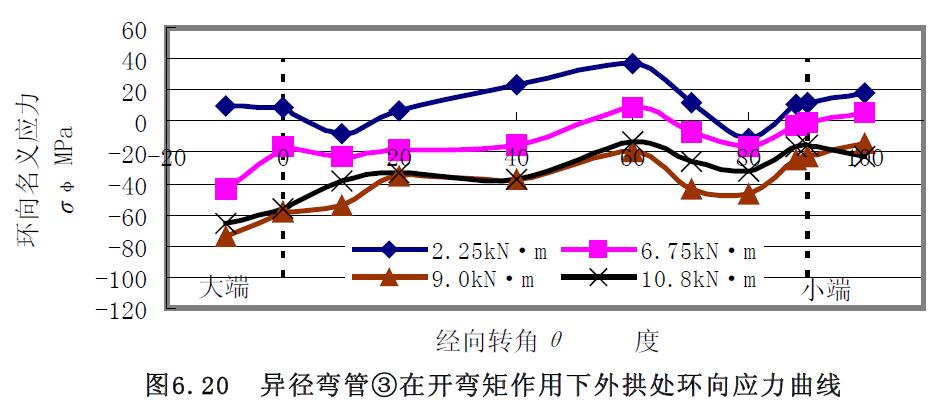
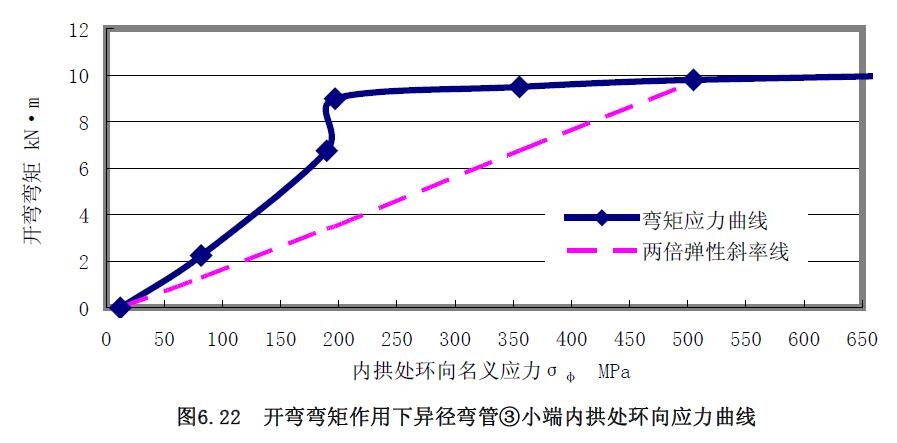
    2) 極限載荷曲線比較分析 對載荷應力曲線圖6.21 和圖6.22 分析可知，開彎矩作用下，異徑彎管③小端內(nèi)拱處外壁面的環(huán)向應力要比經(jīng)向應力大，但兩者較接近，與解析解分析結論一致，求取的極限開彎彎矩分別為10kN·m 和9.9kN·m，相差1%。

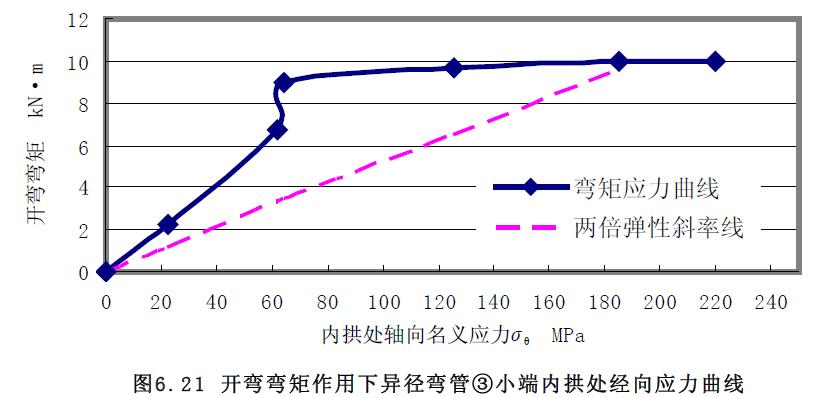
6.3.4 閉彎矩試驗

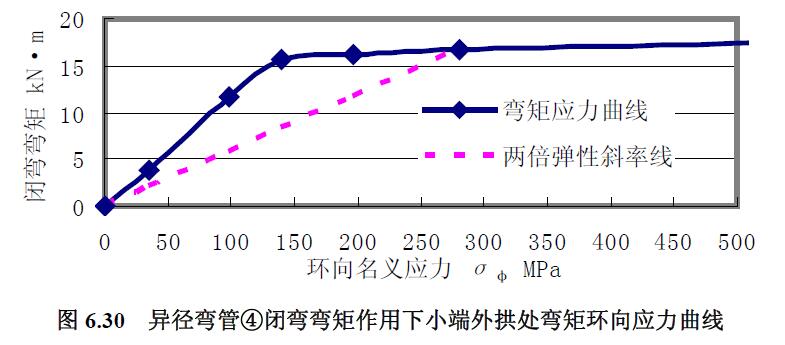
    1) 應力曲線 異徑彎管④和⑥組合試件進行了大端閉彎矩的加載實驗。對于異徑彎管④的應力曲線圖6.23～圖6.28 分析：(1) 環(huán)向應力曲線除外拱上大端附近0°～30°經(jīng)向轉角范圍不變外，其余經(jīng)向轉角及中性線和內(nèi)拱上的環(huán)向應力曲線均隨著彎矩的增大而分散；而經(jīng)向應力曲線只在小端附近70°～90°經(jīng)向轉角范圍隨著彎矩的增大而分散，其余經(jīng)向轉角的經(jīng)向應力曲線基本集中在一起。(2) 中性線的環(huán)向應力和經(jīng)向應力、外拱上的經(jīng)向應力為拉應力，外拱上的環(huán)向應力、內(nèi)拱上的環(huán)向應力和經(jīng)向應力為壓應力。(3) 隨著彎矩的增大，應力的增加幅度也越來越大。(4) 相對而言，中性線上的應力曲線較緩和。

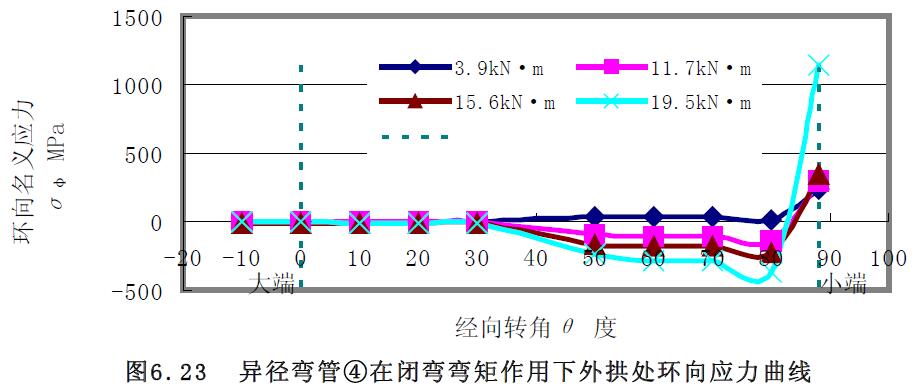
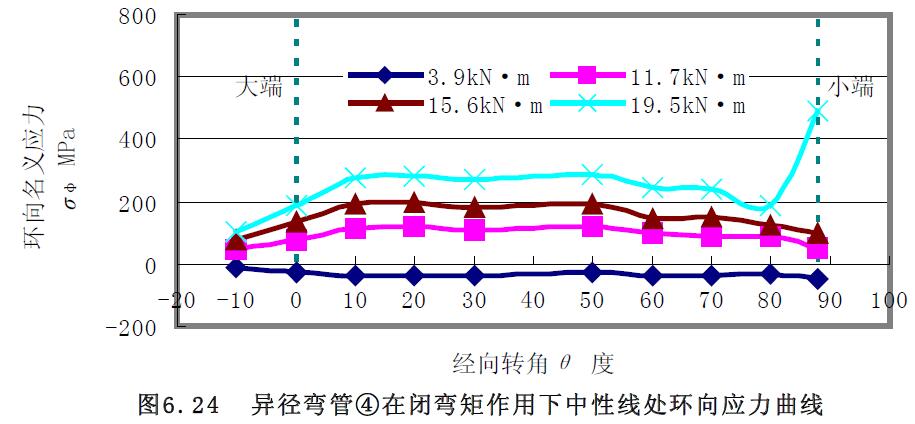
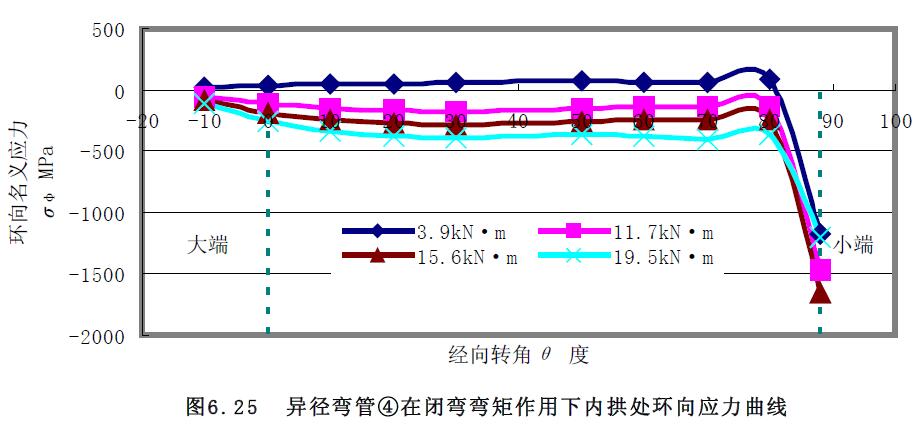
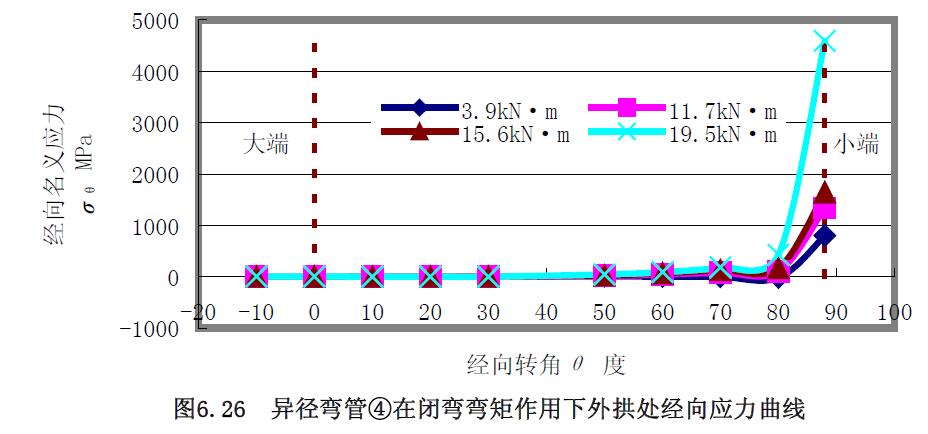
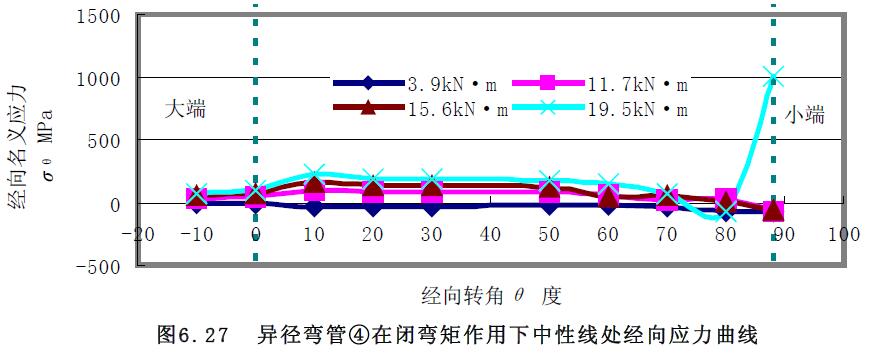
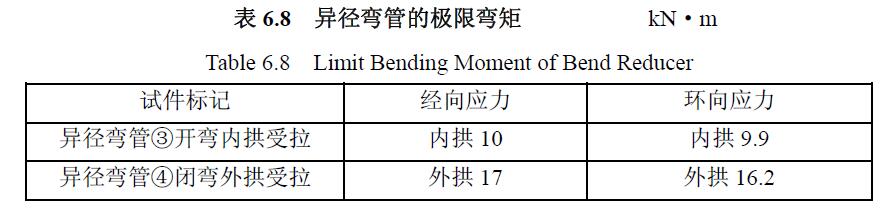
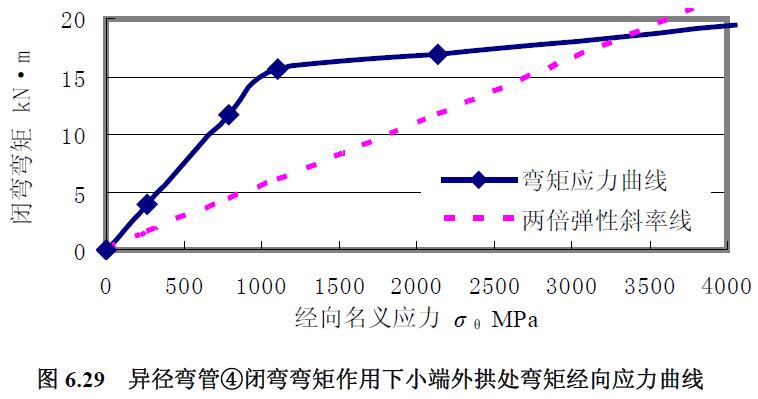
    2) 極限載荷曲線比較分析對閉彎矩作用下載荷應力曲線圖 6.29 至圖6.30 分析，求得極限彎矩如表6.8 所示。

6.3.5 扭矩試驗

    對于異徑彎管①扭矩試驗結果圖6.31 至圖6.40 分析如下。

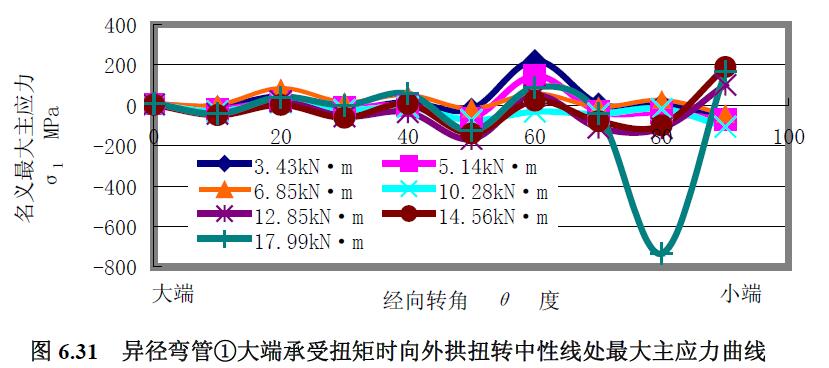
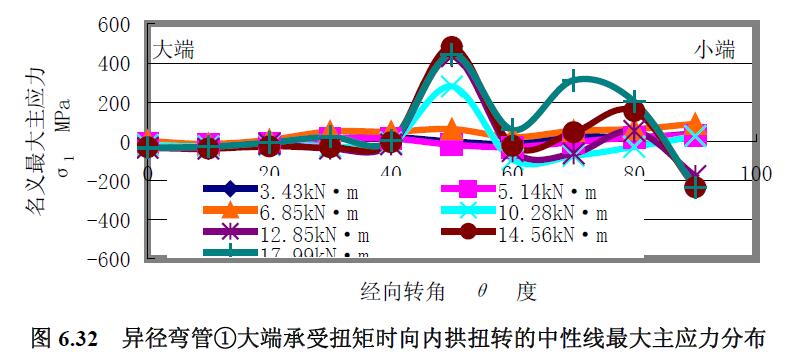
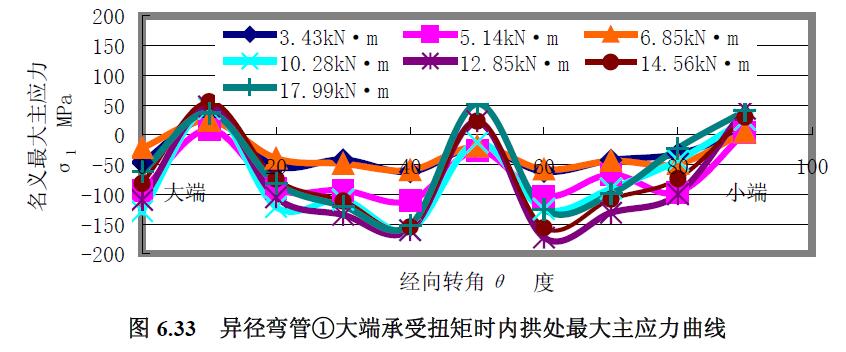
    1) 最大主應力 分析結果：(1) 不同經(jīng)線上的最大主應力曲線區(qū)別較大，除內(nèi)拱上的最大主應力曲線外，均顯出大端的應力曲線較集中，小端的應力曲線較分散；內(nèi)拱上的最大主應力曲線隨扭矩的增大先陡峭后緩和。(2) 從大端到小端，中性線上的最大主應力曲線由集中到分散，向外拱扭轉的中性線應力曲線與向內(nèi)拱扭轉的中性線應力曲線有差別。(3) 從大端到小端，外拱上的最大主應力曲線集中成一條零應力線，較大扭矩下靠近小端才向壓應力分散。(4) 內(nèi)拱上最大主應力水平較低，外拱上靠近小端最大主應力水平較大。

    2) 最小主應力 分析結果：(1) 除外拱上的最小主應力曲線與最大主應力曲線相同外，其他經(jīng)線上的最小主應力曲線與最大主應力曲線區(qū)別較大，最小主應力為壓應力。(2) 向外拱扭轉的中性線上的最小主應力曲線是較平緩和集中的壓應力曲線。(3) 扭矩載荷較低時，向內(nèi)拱扭轉的中性線上的最小主應力曲線也是較平緩的壓應力曲線，隨著扭矩載荷增大，靠近小端段呈波浪變化。(4) 隨著扭矩載荷增大，內(nèi)拱最小主應力曲線越陡峭波浪變化，并且靠近小端段的變化較大。(5) 內(nèi)拱上最大主應力曲線的應力水平較低。

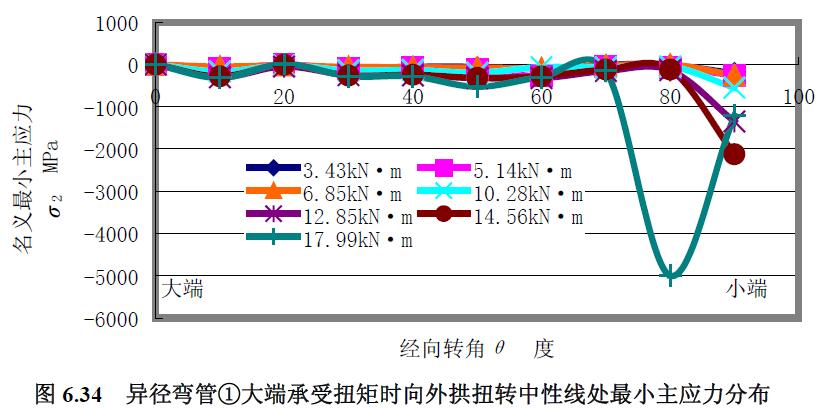
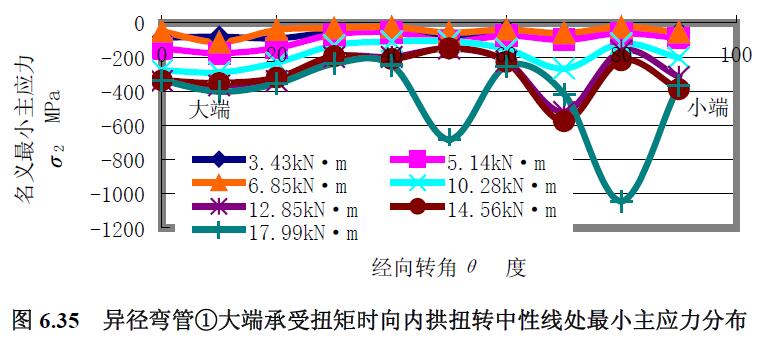
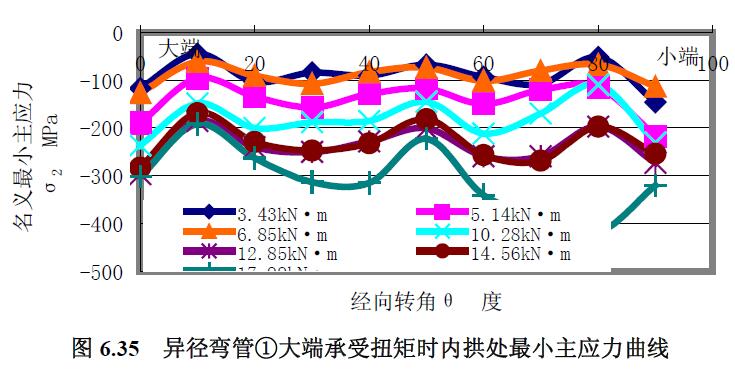
    3) 最大剪應力 分析結果：(1) 最大剪應力曲線與主應力曲線區(qū)別較大，除曲線形狀走勢不同外，最大剪應力均為拉應力。(2) 從0°～40°經(jīng)向轉角范圍內(nèi)，各經(jīng)線上最大剪應力曲線是較平緩的拉應力曲線，除了向外拱扭轉的中性線上的最大剪應力曲線在該段經(jīng)向轉角范圍內(nèi)較集中外，其他各經(jīng)線上的最大剪應力曲線均隨扭矩載荷的增大而分散。(3)外拱上最大剪應力曲線的應力水平較低，內(nèi)拱的較外拱的略大，向外拱扭轉的中性線上靠近小端80°經(jīng)向轉角處的最大剪應力水平較大。(4) 越靠近大端，曲線越集中和緩和。

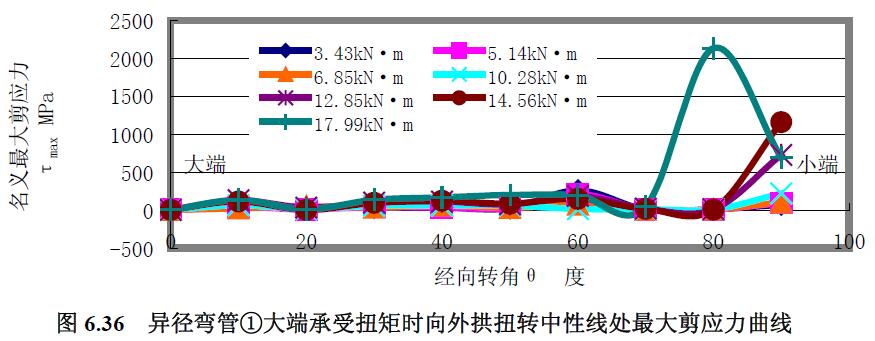
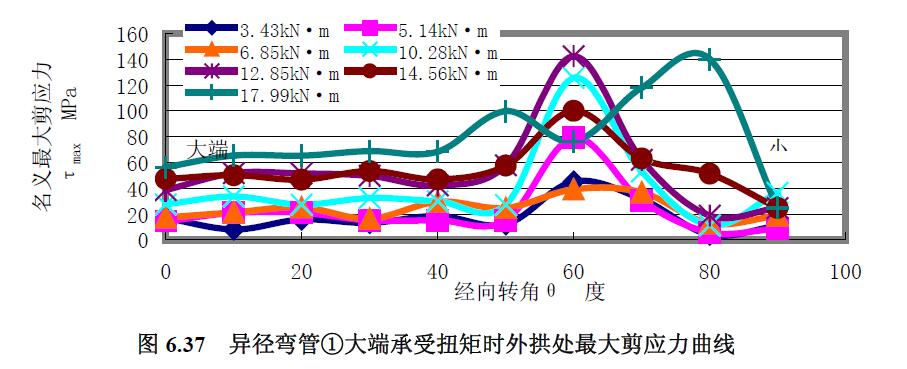
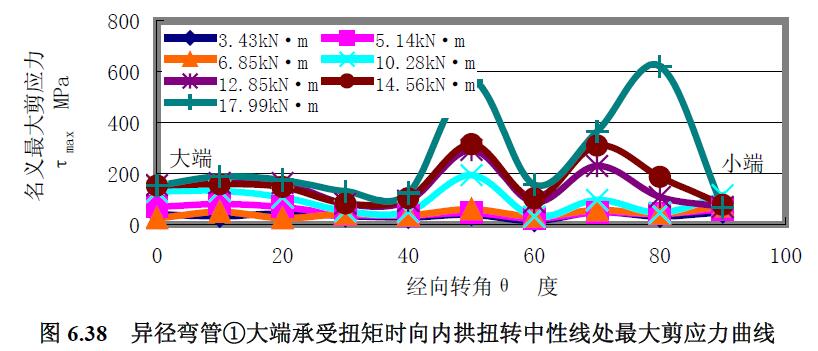
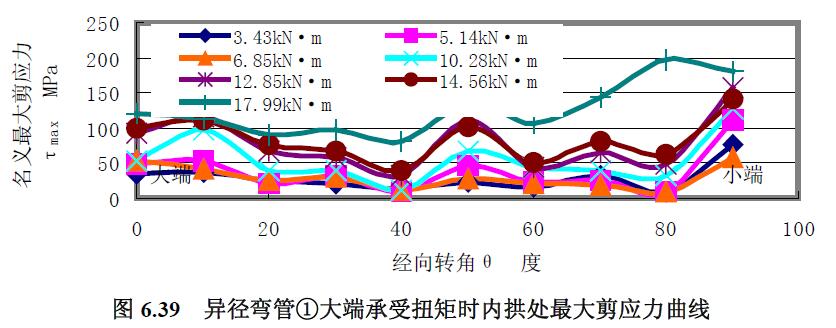
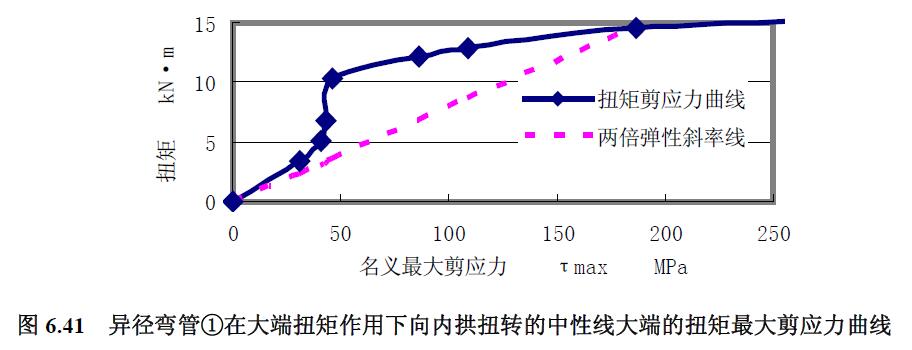
    4) 極限載荷曲線比較分析 分析結果：分析圖6.36～圖6.39 各曲線，與公式(4-52)所表達的異徑彎管大端承受扭矩時其極限扭矩由小端口截面控制的結論一致。由小端的應力變化繪制得扭矩應力曲線如圖6.40～圖6.41，求得異徑彎管①的極限扭矩均為14.6kN·m。